Here we describe the chemical system that is treated by the model (the solid, gas, and liquid phases that can be present), how the properties of organic compounds are specified by the user, and the available methods for estimating activity coefficients in the liquid phase(s). The calculation of densities and surface tensions of the liquid phase(s) is also summarised. References to papers in the peer-reviewed literature are given.
The chemical system that is modelled consists of a gas phase, inorganic and organic solids, and up to two liquid phases. One of these liquid phases is aqueous and can contain both inorganic electrolytes and dissolved organic compounds, and the other phase is hydrophobic and can contain only organic compounds.
The systems treated by the gas/liquid/solid equilibrium model include an arbitrary number of organic components in addition to inorganic electrolytes. These organic compounds can be either water-soluble, for example acids and alcohols, or hydrophobic (such as alkanes and other non-polar compounds). The possible condensed phases in the model system are:
The additional liquid phase can equilibrate with the aqueous phase, and all condensed phases can equilibrate with the gas phase.
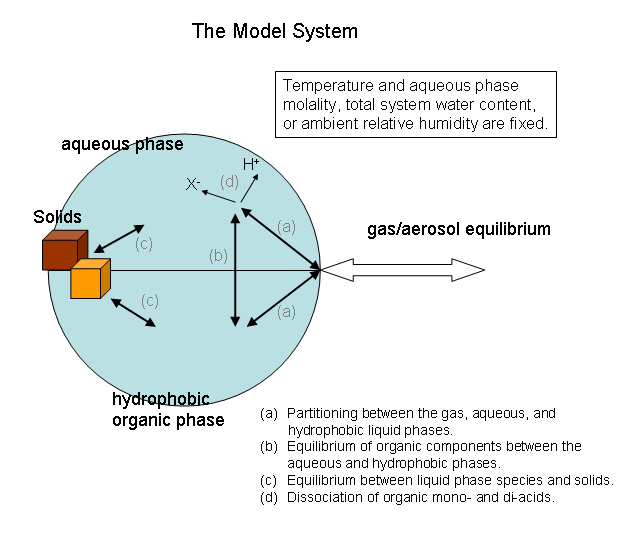
The modelled system is shown in the figure below, and corresponds to that described by Clegg et al. (1). The organic compounds present in the modelled system, and their properties, can be defined by the user. Individual organic compounds are allowed to partition between both aqueous and hydrophobic phases, or can be constrained by the user to exist in only one of the two phases. Each of the equilibria indicated by the arrows in the figure can be switched on or off for individual organic components.
Ions and water are not able to partition into the hydrophobic phase in the model.

Although the figure shows the model system as an aerosol droplet in equilibrium with the surrounding atmosphere, the calculation (and the results) are the same as would be obtained for a bulk system. Aerosol size effects, which act to increase the equilibrium partial pressures of water and volatile components for particles of less than about 0.1 μm in diameter, are not yet included in the model.
For systems not containing organic compounds the model behaves in the same way as those previously on this site. However, we have added the dissociation of NH4+, and of H2O, which allows the models to be applied to neutral and alkaline systems.
For each calculation users can either select compounds from a library which is provided, or define new compounds and their thermodynamic properties. These properties include:
Organic compounds are chosen and/or defined for a calculation on the Available Compounds page which can be accessed from each model calculation page and from the E-AIM home page. The set of selected organic compounds can be changed at any time during the user's session, and the thermodynamic properties of the compounds can also be modified as required.
It is a common assumption in aerosol science that particles remain in a liquid, metastable, state even at low relative humidities when solute concentrations are very high and the solutions supersaturated. In atmospheric aerosol particles the organic phase is likely to contain very many components and it is also usual to treat this as a supercooled liquid rather than a collection of individual or mixed solids. For this reason one of the thermodynamic quantities that users can specify for organic compounds in the model is the vapour pressure of the (supercooled) liquid organic compound. Unless the activity product of the organic compound in a saturated aqueous solution is also specified (allowing the formation of the solid to be calculated) the compound will always exist as a solute in the aqueous phase and/or as a component in the hydrophobic liquid organic phase.
Users who register with the E-AIM site - a simple process which takes only a few minutes - can save any compounds that they define in their own private library. These compounds will be available to them next time they log in. Users can also make their compounds available for use by others, for example research colleagues or classes of students.
Users who do not register with the site can carry out all types of calculations, but any organic compounds they define only remain available until the end of the user's session (which generally lasts until they close their browser), and are not saved.
Equilibria between the liquid (aerosol) phases and the gas phase, and the formation of solids, are determined by both the concentrations of the species in the aerosol phase, and their activity coefficients. This section summarises how activity coefficients are estimated in the model, and the choices available to the user.
3a. Aqueous inorganic and organic electrolyte solutionsCalculations of the activities of water and ions present in the aqueous aerosol utilise the Pitzer, Simonson and Clegg equations (2). The current models build on previous applications to aqueous H2SO4 and HNO3, and to their mixtures with HCl and HBr (3-5). More recent results, incorporated into the models on this site, are the subject of several papers (6-9, 18). Some current developments (also present in the models on the site) are summarised on the web pages that describe Model II and Model III.
Organic anions produced by the dissociation of organic acids, and cations produced by the reaction of amines with H+, are also treated by the Pitzer, Simonson and Clegg equations within E-AIM. Because there are insufficient data to determine interaction parameters for these ions we assign cation - anion interaction parameters in the following way:
These assumptions are likely to be more accurate than using only the Debye-Huckel limiting law, which would result in very low predicted activity coefficients at all concentrations. Values of Mg2+ - Cl− and Mg2+ - SO42− interaction parameters were obtained by fitting the activity coefficient model to published data at 25 °C (refs. 24 - 28), and are used at all temperatures. The measurements include data for highly concentrated solutions, supersaturated with respect to the magnesium salts. The requirements of the fits for such solutions (that they yield predicted water activities which monotonically decrease with concentration to x(Salt) = 1.0) mean that activity coefficients in the most concentrated solutions may be overestimated.
No ternary (mixture) parameters such as Wii'j and Qn,ii'j are assigned for organic ions. This assumption will be most accurate in dilute solutions.
3b. Aqueous solutions of organic compoundsIn E-AIM, the following activity coefficient models can be applied to mixtures of uuncharged organic compounds dissolved in water:
Raoult's law is the simplest possible assumption: that the mole fraction activity coefficient of the organic component, relative to a reference state of the pure liquid, is equal to unity under all conditions.
The Redlich-Kister equation (10,11), using up to 10 fitted parameters, can be used to represent activity coefficients in solutions of single organic compounds in water. The parameters cannot be varied with temperature, and therefore the predicted activity coefficients using this model are also invariant with temperature.
The value of this equation is that, for solutions for which data are available, it can be used to represent water and solute activities very accurately. Its disadvantage is that it can only be used for mixtures of two miscible components - for single organic solutes in water - and the properties of mixtures are estimated as described further below. Examples of the use of the Redlich-Kister equation to fit measured activities of aqueous dicarboxylic acids in water are given by Clegg and Seinfeld (11). The equation is given here, and in the help pages for entering organic thermodynamic properties in E-AIM.
UNIFAC can be used for mixtures of water and multiple organic solutes, and also for mixtures of organic compounds that do not contain water. Both the standard UNIFAC parameter set (12), and the modified parameters of Peng et al. (13), are provided. In UNIFAC the activity coefficients of the mixture components are determined by interactions of the structural groups that make up each component. The user must provide the structural group composition of each molecule that is to be treated by UNIFAC (unless the compound is present in the library provided.) Click here for a list of all the UNIFAC structural groups and examples of their use.
The choice of equation is made, for each organic compound, on the data entry page for its thermodynamic properties. If the Redlich-Kister equation is used then values of the fitted parameters must be entered; if UNIFAC is chosen the structural group compostion of the molecule must be entered.
3c. Aqueous solutions containing electrolytes and organic compoundsSolute and solvent activities in aqueous solutions containing both organic and inorganic solutes are approximated using the method proposed by Clegg et al. (14). This assumes that the inorganic ions and organic solutes do not influence each other. Consequently their activity coefficients, expressed on a molality basis, are equal to those calculated for the systems water + inorganic ions only, and water + organic solutes only. The water activity coefficient of the mixture, aW(mix), is given by:
aW(mix) = aW(inorg) × aW(org)
where aW(inorg) is the calculated water activity for water + ions only and aW(org) is the calculated water activity for water + organic compounds only. This is thermodynamically consistent with the treatment of the activity coefficients, and is equivalent to equation (3) of ref. (14) which is expressed in terms of the osmotic coefficient of the solution. We note that this water activity is not the same as would be obtained using the Zdanovskii-Stokes-Robinson method of estimating solution water content. See Clegg and Seinfeld (11) for examples of the application of both approaches.
Users should be aware that this simplified treament of inorganic/organic mixtures is an approximation which does not attempt to model "salting-in" and "salting-out" behaviour (e.g., ref. 15).
3d. Organic compounds in the hydrophobic phaseThe modelled system can also contain a hydrophobic phase, where non-polar compounds such as alkanes are expected to reside. Such a phase would contain extremely small amounts of water, but this is neglected in E-AIM for the sake of computational simplicity. Two activity coefficient equations are provided:
The choice of equation is made, for each organic compound, on the data entry page for its thermodynamic properties.
The Zdanovskii-Stokes-Robinson (ZSR) equation (16,17) is a robust, and commonly used, method for estimating aerosol water content for known atmospheric relative humidity (equivalent to aerosol phase water activity). Options have been added to the model so that ZSR calculations can be carried out for some systems. Consider an aqueous phase containing inorganic ions, water, and 6 organic compounds Org(1) to Org(6). Their activities in aqueous solution, for this example, are described as follows:
Org(1): Raoult's law
Org(2): Redlich-Kister equation
Org(3): Redlich-Kister equation
Org(4) + Org(5) + Org(6): UNIFAC
Using the approximation of Clegg et al. (14) the water activity of the mixture aW(mix) is given by:
aW(mix) = aW(ions) × aW(Org[1]) × aW(Org[2]) × aW(Org[3]) × aW(Org[4-6])
where each water activity is calculated, using the specified model, for a solution containing the amount of water in the mixture plus the indicated solutes only. The solute activity coefficients are calculated for the same individual solutions and are used in the model unchanged except for converting the mole fraction activity coefficients to a mixture basis.
When the user specifies total water content of a chemical system E-AIM calculates the water activity, aW(mix). Conversely, when the ambient relative humidity (which is equivalent to the water activity in a system at equilibrium) is given as an input, the model calculates the water content of the system in both the gas and condensed phases.
The E-AIM model will also determine a value for the equilibrium relative humidity that would obtained using ZSR, for the total amount of liquid water in the system. This calculation is only carried out for systems containing both inorganic and organic compounds in the aqueous phase. For systems that are dilute aqueous solutions both relative humidities (or water activities) will be similar, but in more concentrated solutions which have lower water activities the results of the two methods will diverge.
On the E-AIM model pages for 'Comprehensive' calculations it is possible to specify whether organic components are treated as single components, as Org(1) to Org(3) are in the example above, or using the ZSR relationship. If ZSR is selected for two or more components both the water activity and solute activity coefficients for those components are calculated using the ZSR relationship. For example, if this was done for Org(1) to Org(3) then the equation for aW(mix) would be:
aW(mix) = aW(ions) × aW{(Org[1-3]), ZSR} × aW(Org[4-6])
For systems in which no ions are present, a 'pure' ZSR model calculation of both water activity and solute activity coefficients in the mixture can be carried out by selecting the ZSR option for all organic compounds. The default is that organic compounds are treated as single components (if Raoult's law or the Redlich-Kister equation is used to calculate activity coefficients), or are grouped together if UNIFAC is chosen (as in the example above for Org(4) to Org(6)).
For compounds in the hydrophobic phase such choices do not arise: the system is treated as a mixed solvent system and activity coefficients are either unity (if Raoult's law is chosen) or are calculated by UNIFAC.
(1) Density. The method of Tang, as formulated by Semmler et al.(20), is used to estimate the densities of mixtures from those of solutions containing single electrolytes or dissolved organic compounds, as described in the Appendix of Clegg and Wexler (19). Values of densities of inorganic electrolyte solutions were calculated using the equations of Clegg and Wexler (19), which extend to the supercooled liquid state and supersaturation with respect to dissolved electrolytes. Densities of inorganic solids are taken from their Table 16.
Solutions that contain dissolved organic compounds are treated as follows. First, densities of their pure aqueous solutions are calculated by assuming that the apparent molar volumes of the compounds, at all concentrations and temperatures, are equal to the molar volumes (at 298.15 K) input by the user. Note that, if no measured molar volumes or densities are available for the pure liquid organic compounds, they can be predicted using the calculator on this site. If no molar volume(s) are entered for one or more of the organic compound(s) then E-AIM will not attempt to estimate the density of the solution.
Second, if the organic compounds in solution are acids or amines then there may be significant concentrations of organic ions in the aqueous phase. The apparent molar volumes of these ions, at infinite dilution in water, are assumed to be the same as those of the parent acid or amine (and also to be invariant with temperature). When calculating the effect of these ions on solution density they are combined with the same property of the other ions of opposite charge that are present to form electrolytes. For example, consider a solution of NaCl containing a dissociating organic acid HX. If the assumed molar volume of organic anion X− is 20 cm3 mol−1, then the apparent molar volume of the electrolyte NaX which is used in the estimation of mixture density is 20 + (-1.2) = 18.8 cm3 mol−1 in all solutions containing both ions. The value of -1.2 cm3 mol−1 is the apparent molar volume of Na+ at infinite dilution in water at 298.15 K.
Only undissociated organic compounds can exist in the organic liquid phase. The density of this phase is also estimated using the method of Semmler et al. (20), using the molar volumes of the pure liquid organic compounds that have been input by the user. If any of the molar volumes are not available, because they haven't been entered, E-AIM will not estimate the density of the phase.
Molar volumes of organic solids or hydrates can be entered by the user on the data page for each organic compound.
(2) Surface tension. The surface tension of the aqueous phase, including organic solutes, is calculated using the model of Dutcher et al. (21). Model parameters for organic solutes must be entered by the user. The model assumes that all solutes are fully mixed within the aqueous phase, and is therefore not suitable for "surface active" compounds that may concentrate at the surface of the bulk solution or droplet which magnifies their effects. The influence of organic cations and anions on surface tension are assumed to be zero. This assumption, which is necessary because of the lack of data, is likely to be reasonable only when the concentrations of the ions are low relative to those of other solution components. The "verbose" form of model output therefore lists the mole percentage in solution of all electrolytes containing organic ions for which this assumption is made. The user should be cautious about using results in these cases.
Surface tensions of the organic phase can also be estimated using the model of Dutcher et al. (21), where the parameters have been entered by the user (see the help page for a description). If no parameters have been entered for one or more of the organic species then no surface tension will be estimated.
Petters and Kreidenweis (22) have developed an approximate description of the water uptake of soluble material, and its dependence upon ambient relative humidity, based upon the parameter κ. It is defined by their eq (3), and associated equations, so that:
κ = Vw / Vs × (1 − RH) / RH
where Vw is the volume of water in which the solutes are dissolved, and Vs the total 'dry' volume of the solutes. (The volume of water, for the purposes of this calculation, is simply equal to the total volume of the solution less the volume of dry solutes.) Because κ is an approximate parameter, the values calculated from E-AIM results will be different at every RH and temperature even if the chemical composition of the system remains the same.
The κ in the equation above applies to the whole solution, which might contain an indefinite number of inorganic and organic solutes, and it is this value that is given in the E-AIM results. Note that equation (7) of Petters and Kreidenweis expresses the parameter as the weighted sum of the values for the individual solutes, thus: κ = Σi (εi κi), where εi is the volume fraction of solute component i in the mixture (equal to Vsi / Vs). This relationship implies simple additivity of the amounts of water associated with each solute in solution (eq 4 of Petters and Kreidenweis), which is not consistent with the generally more accurate methods in E-AIM. However, differences are likely to be small, and lowest at high relative humidities.
The total volume of 'dry' solutes in the above equation, Vs, is calculated in E-AIM in the following way. For the inorganic components of the solution all possible solids containing one cation and one anion are assumed to be formed. For example, in a chemical system containing NH4+, Na+, SO42−, and Cl− the following dry solid solutes would occur: (NH4)2SO4, Na2SO4, NH4Cl, and NaCl.
In acidic particles, which also contain SO42−, H2SO4 will be predicted to exist. In such cases, if NH4+ and/or Na+ are also present, then it is assumed that the maximum possible amounts of the bisulphates NaHSO4 and NH4HSO4 (in that order) will be formed, in preference to the acid. If any H2SO4 remains, after assignment to these acid salts, then its density and molar volume are assumed to have the values listed in Table 1 on the page describing the inputs for Köhler calculations. (The assumed volume properties of HNO3 and HCl are also listed in the same table.) The amounts of the individual inorganic salts and acids, after the assignment of the bisulphates, are calculated using eq (4) of Clegg and Simonson (23) which implements a simple mixing rule.
The contributions to Vs of any organic compounds present are relatively simple: if the organic compound can form a solid (specified on the Available Compounds pages), then its molar volume will be used; if no solid is specified for the compound then the molar volume of the liquid organic will be employed instead. In the cases of organic acids and amines, both of which take part in association/dissociation reactions in solution, the molar volumes used in the calculation of Vs are those of the molecular forms.
There are a number of circumstances in which κ is not calculated, chiefly related to the need to be able to estimate the dry volume (Vs) of the solutes present. First, for the inorganic component of the chemical system:
The equilibrium state of the system is calculated by minimisation of the Gibbs energy, With the addition of organic compounds the chemical system being treated is significantly more complex, and there are opportunities for users to specify unreasonable or unfeasible systems. A simple example of this would be defining an organic compound which, according to the activity coefficient model, undergoes a phase separation in water. If the user restricted this compound to exist only in the aqueous phase then the minimisation algorithm might be unable to find a solution, and the results would anyway be erroneous.
Extensive checking of each result is carried out by the system, to determine that gas/liquid/solid equilibrium for each species satisfies the appropriate equation and equilibrium constant. This tests the self consistency of the result, although it is not a guarantee of accuracy, and errors are flagged if found. In most cases this will enable the problem to be redefined, so that it can be run again successfully.
Contact the authors of the model if you encounter results you do not understand, or apparent failures of the model that cannot be resolved.
(1) S. L. Clegg, M. J. Kleeman, R. J. Griffin, and J. H. Seinfeld (2007) Effects of uncertainties in the thermodynamic properties of aerosol components in an air quality model - Part I: Treatment of inorganic electrolytes and organic compounds in the condensed phase. Atmos. Chem. Phys. 8, 1057-1085.
(2) S. L. Clegg, K. S. Pitzer and P. Brimblecombe (1992) Thermodynamics of multicomponent, miscible, ionic solutions. II. Mixtures including unsymmetrical electrolytes. J. Phys. Chem. 96, 9470-9479; 1994, 98, 1368; 1995, 99, 6755.
(3) S. L. Clegg and P. Brimblecombe (1995) Application of a multicomponent thermodynamic model to activities and thermal properties of 0 - 40 mol kg-1 aqueous sulphuric acid from <200 K to 328 K. J. Chem. Eng. Data 40, 43-64.
(4) S. L. Clegg and P. Brimblecombe (1990) Equilibrium partial pressures, and mean activity and osmotic coefficients of 0-100% nitric acid as a function of temperature. J. Phys. Chem. 94, 5369-5380; 96, 6854.
(5) K. S. Carslaw, S. L. Clegg, and P. Brimblecombe (1995) A thermodynamic model of the system HCl - HNO3 - H2SO4 - H2O, including solubilities of HBr, from <200 K to 328 K. J. Phys. Chem. 99, 11557-11574.
(6) S. L. Clegg, P. Brimblecombe and A. S. Wexler (1998) A thermodynamic model of the system H - NH4 - SO4 - NO3 - H2O at tropospheric temperatures. J. Phys. Chem. A 102, 2137-2154.
(7) S. L. Clegg, P. Brimblecombe and A. S. Wexler (1998) A thermodynamic model of the system H - NH4 - Na - SO4 - NO3 - Cl - H2O at at 298.15 K. J. Phys. Chem. A 102, 2155-2171.
(8) M. Massucci, S. L. Clegg, and P. Brimblecombe (1999) Equilibrium partial pressures, thermodynamic properties of aqueous and solid phases, and Cl2 production from aqueous HCl and HNO2 and their mixtures. J. Phys. Chem. A 103, 4209-4226.
(9) A. S. Wexler, and S. L. Clegg (2002) Atmospheric aerosol models for systems including the ions H, NH4, Na, SO4, NO3, Cl, Br and H2O, J. Geophys. Res. 107, No. D14, art. no. 4207, 14 pages.
(10) M. L. McGlashan (1963) Deviations from Raoult's law. J. Chem. Educ. 40, 516-518.
(11) S. L. Clegg and J. H. Seinfeld (2006) Thermodynamic models of aqueous solutions containing inorganic electrolytes and dicarboxylic acids at 298.15 K. 1. The acids as nondissociating components. J. Phys. Chem. A 110, 5692-5717.
(12) R. Wittig, J. Lohmann, and J. Gmehling (2003) Vapor-liquid equilibria by UNIFAC group contribution. 6. Revision and extension. Ind. Eng. Chem. Res. 42, 183-188.
(13) C. Peng, M. N. Chan, and C. K. Chan (2001) The hydgroscopic properties of dicarboxylic and multifunctional acids: measurements and UNIFAC predictions. Environ. Sci. Technol. 35, 4495-4501.
(14) S. L. Clegg, J. H. Seinfeld, and P. Brimblecombe (2001) Thermodynamic modelling of aqueous aerosols containing electrolytes and dissolved organic compounds. J. Aerosol Sci. 32, 713-738.
(15) F. J. Millero (2001) Physical Chemistry of Natural Waters, Wiley-Interscience, 654 pp.
(16) R. H. Stokes, and R. A. Robinson (1966) Interactions in aqueous non-electrolyte solutions. 1. Solute- solvent equilibria. J. Phys. Chem. 70, 2126-2130.
(17) S. L. Clegg, and J. H. Seinfeld (2004) Improvement of the Zdanovskii-Stokes-Robinson model for mixtures containing solutes of different charge types. J. Phys. Chem. A 108, 1008-1017.
(18) E. Friese and A. Ebel (2010) Temperature dependent thermodynamic model of the system H+ - NH4+ - Na+ - SO42− - NO3− - Cl− - H2O. J. Phys. Chem. A, 114, 11595-11631.
(19) S. L. Clegg and A. S. Wexler (2011) Densities and apparent molar volumes of atmospherically important electrolyte solutions. I. The solutes H2SO4, HNO3, HCl, Na2SO4, NaNO3, NaCl, (NH4)2SO4, NH4NO3, and NH4Cl from 0 to 50 °C, including extrapolations to very low temperature and to the pure liquid state, and NaHSO4, NaOH and NH3 at 25 °C. J. Phys. Chem. A 115, 3393-3460.
(20) M. Semmler, M.; B. P. Luo; and T. Koop (2006) Densities of H+ / NH4+ / SO42− / NO3− / H2O liquid solutions at tropospheric temperatures. Atmos. Environ. 40, 467–483.
(21) C. S. Dutcher, A. S. Wexler and S. L. Clegg (2010) Surface tensions of inorganic multicomponent aqueous electrolyte solutions and melts. J. Phys. Chem. A, 114, 12216-12230.
(22) M. D. Petters and S. M. Kreidenweis (2007) A single parameter representation of hygroscopic growth and cloud
condensation nucleus activity. Atmos. Chem. Phys. 7, 1961-1971.
(23) S. L. Clegg and J. M. Simonson (2001) A BET model of the thermodynamics of aqueous
multicomponent solutions at extreme concentration. J. Chem. Thermodyn. 33, 1457-1472.
(24) Z. Ha and C. K. Chan (1999) The water activities of
MgCl2, Mg(NO3)2,
MgSO4, and their
mixtures Aerosol Sci. & Technol., 31, 154-169.
(25) K. S. Pitzer, P. Wang, J. A. Rard, and S. L. Clegg (1999)
Thermodynamics of electrolytes. 13. Ionic strength dependence
of higher order terms; equations for CaCl2 and
MgCl2. J. Solut. Chem., 28, 265-282.
(26) J. A. Rard, and D. G. Miller (1981) Isopiestic determination of osmotic and activity coefficients
of aqueous MgCl2 solutions at 25 ° C. J. Chem. Eng. Data, 26, 33-38.
(27) R. A. Robinson and R. H. Stokes (1970) Electrolyte Solutions, 2nd Edn., Butterworth & Co., London.
(28) I. N. Tang, A. C. Tridico, and K. H. Fung (1997) Thermodynamic and optical properties of seasalt aerosls. J. Geophys. Res., 102D, 23269-23275.